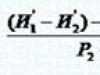Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель урока. Решение уравнений с параметрами и модулями, применяя свойства функций в неожиданных ситуациях и освоение геометрических приемов решения задач. Нестандарные уравнения.
Задачи:
- Образовательные : научить решать некоторые виды уравнений уравнений модулями и параметрами;
- Развивающие : развивать культуру мысли, культуру речи и умение работать с тетрадью и доской.
- Воспитательные : воспитывать самостоятельность и умение преодолевать трудности.
Оборудование: наглядный материал для устного счёта и объяснения новой темы. Интерактивная доска, мультимедийное оборудование урока.
Структура урока:
- Повторение изученного материала (устный счёт).
- Изучение нового материала.
- Закрепление изученного материала.
- Итог урока.
- Домашнее задание.
ХОД УРОКА
1. Повторение важнейшего теоретического материала по темам: «Уравнения, содержащие модуль», «Решение уравнений с параметрами»
1) «Уравнения, содержащие модуль»
Абсолютной величиной или модулем числа a называется число a , если a > 0, число – a , если a < 0, нуль, если a = 0. Или
Из определения следует, что | a
| >
0
и | a
| >
a
для всех a
€ R .
Неравенство | x
| < a
, (если a
> 0) равносильно двойному неравенству – a
<
х
< a
.
Неравенство | x
| < a
, (если a
< 0)
не имеет смысла, так как | х | >0.
Неравенство | x
| > a
, (если a
> 0)
равносильно двум неравенствам
Неравенство | x
| > a
, (если a
< 0)
справедливо для любого х
€ R.
2) «Решение уравнений с параметрами»
Решить уравнение с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они.
а) определить множество допустимых значений неизвестного и параметров;
б) для каждой допустимой системы значений параметров найти соответствующие множества решений уравнения.
2. Устные упражнения
1. Решить уравнение | x – 2 | = 5; Ответ : 7; – 3
| x – 2 | = – 5; Ответ : решения нет
| x – 2 | = х + 5; Ответ : решения нет; 1,5
| x – 2 | = | x + 5 |; Ответ : решения нет; – 1,5; решения нет; – 1,5;
2. Решить уравнение: | x + 3 | + | y – 2 | = 4;
Расcмотрим четыре случая
| { | x + 3 > 0 | { | x > – 3 |
| y – 2 > 0 | y > 2 | ||
| x + 3 + y – 2 = 4 | y = – x + 3 |
| { | x + 3 > 0 | { | x > – 3 |
| y – 2 < 0 | y < 2 | ||
| x + 3 – y + 2 = 4 | y = x + 1 |
| { | x + 3 < 0 | { | x < – 3 |
| y + 2 > 0 | y > – 2 | ||
| – x – 3 – y – 2 = 4 | y = x + 9 |
| { | x + 3 < 0 | { | x < – 3 |
| y + 2 < 0 | y < – 2 | ||
| – x – 3 – y – 2 = 4 | y = – x – 9 |

В результате мы получаем квадрат, центр которого (–3; 2), а длина диагонали равна 8, причем диагонали параллельны осям координат.
Из наглядных соображений можно сделать вывод: что уравнение вида | х + a | + | у + b | = с ; задает на плоскости квадрат с центром в точке (– а ; – b ), диагоналями параллельными осям OX и ОУ, и длина каждой диагонали равна 2с . Ответ : (– 3; 2).
2. Решить уравнение aх = 1
Ответ : если a = 0, то нет решения; если a = 0, то х = 1/ a
3. Решить уравнение (а 2 – 1) х = а + 1.
Решение .
Нетрудно сообразить, что при решении этого уравнения достаточно рассмотреть такие случаи:
1) а = 1; тогда уравнение принимает вид ОX = 2 и не имеет решения
2) а = – 1; получаем ОX = О, и очевидно х – любое.
1
3) если а
= +
1, то х
= –––
а
– 1
Ответ:
если а
= – 1, то х
– любое;
если а
= 1, то нет решения;
1
если а
= +
1 , то х
= –––
а
– 1

3. Решения примеров (из вариантов С)
1. При каком значении параметра р уравнение | х 2 – 5х + 6 | + | х 2 – 5х + 4 | = р имеет четыре корня.
Рассмотрим функцию у = | х 2 – 5х + 6 | + | х 2 – 5х + 4 |
Так как х 2 – 5х + 6 = (х – 2)(х – 3) и х 2 – 5х + 4 = (х – 1)(х – 4), то y = | (х – 2)(х – 3) | + | (х – 1)(х – 4) |, корни квадратных трехчленов отметим на числовой прямой
1 2 3 4 х
Числовая прямая при этом разбивает на 5 промежутков
| { | x < 1 | { | x < 1 |
| y = x 2 – 5x + 6 + x 2 – 5x + 4 | y = 2x 2 – 10x + 10 |
| { | 1 < x < 2 | { | 1 < x < 2 |
| y = x 2 – 5x + 6 – x 2 + 5x – 4 | y = 2 |
| { | 2 < x < 3 | { | 2 < x <3 |
| y = – 2x 2 + 10x – 10 | y = – x 2 + 5x – 6 – x 2 + 5x – 4 |
| { | 3 < x < 4 | { | 3 < x < 4 |
| y = 2 | y = x 2 – 5x + 6 – x 2 + 5x – 4 |
| { | x > 4 | { | x > 4 |
| y = 2x 2 – 10x + 10 | y = x 2 – 5x + 6 + x 2 –5x + 4 |
Для случая 3) х 0 = – b | 2a = 2, y 0 = 25: 2 + 25 – 10 = 2,5
Итак, (2,5; 2,5) – координаты вершины параболы y = – 2x 2 + 10x – 10.
Построим график функции, заданной равенством

Как видно из рисунка, исходное уравнение имеет четыре корня, если 2 < а < 2,5
Ответ : при 2 < а < 2,5
4. Самостоятельная работа по уровням
1 уровень
1. Решить уравнение х
2 – | x
| = 6
2. При каких целых значениях а имеет единственное
решение уравнение ах
2 – (а
+ 1) + а
2
+ а
= 0?
2 уровень
1. Решить уравнение: | x
– 5 | – | 2x
+ 3 | = 10
а
–12) х
2 + 2 =
2(12 – а
) имеет два различных корня?
3 уровень
1. Решить уравнение | x
– 5 | – | 2x
+ 3| = 10
2. Найти все значениях параметра а, при
которых уравнение (а
– 12) х
2 + 2 = 2(12
– а
) имеет два различных корня?
5. Итог урока
1. Определение модуля.
2. Что значит решить уравнение с параметром?
6. Задание на дом. C5 варианта №11 Ф.Ф. Лысенко. Математика, 2012
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
«Линейное уравнение с двумя переменными» - Равенство, содержащее две переменные, называется уравнением с двумя переменными. -Что называется уравнением с двумя переменными? Приведите примеры. -Какое уравнение с двумя переменными называется линейным? Линейное уравнение с двумя переменными. Определение: Алгоритм доказательства, что данная пара чисел является решением уравнения:
«Решение показательных уравнений» - Сведение к одному основанию. Вынесение за скобки. Т. Виета. Графический способ. Показательным уравнением называют уравнение, содержащее переменную в показателе степени. Решение показательных уравнений. Устная работа. ab+ac=a(b+c). Степени. 2.Решить уравнение: Свойство. Виды и способы решения показательных уравнений.
«Графический способ решения уравнений» - Ответ: один корень, х=-1. Два корня. Решить графически уравнение (х+1)/(х-2)=2. Построить график функции y=x?+6x+8. Практикум по решению уравнений графическим способом Подготовка к зачету. Построить графики функций. Построить график функции y=(x+1)/(x-2). 1. Перенесем 8 в правую часть уравнения. Корней нет.
«Решение целых уравнений» - «Уравнения, в которых скопом Корни, степень, неравенств бездна. Три великих математика. Удачи в дальнейшем изучении методов решения уравнений. Осевая симметрия присуща большинству видов растений и животных. Центральная. В животном мире 2 вида симметрии. Диктант. Осевая. Определите методы решения уравнений.
«Уравнения с логарифмами» - Логарифмические уравнения. Реши устно уравнения. Формулы преобразования логарифмов. Уравнение. Определение. Таблицы логарифмов. Определение логарифма. Определение и свойства логарифма. Логарифмическая линейка. Функция. Наушники или колонки. Область определения. Подходы к решению. Решить уравнение. Гимназия.
«Иррациональные уравнения» - На контроль д/з выполнили: №419 (в,г) Сафиуллина, №418(в,г) Кульмухаметов, №420(в,г)Шагеев. 2 урок Решение систем уравнений. Урок 1 Тема: Решение иррациональных уравнений. 1.Какие из следующих уравнений являются иррациональными: Цели: Познакомить учащихся с решениями некоторых видов иррациональных уравнений.
Всего в теме 49 презентаций
Как говорили древние философы «Мудрость – это любовь к знаниям, а любовь – это мера всех вещей». «Мера» на латинском языке - «modulus», от него и произошло слово «модуль». И сегодня мы с вами поработаем с уравнениями, содержащими модуль. Надеюсь, у нас все получится, и в конце урока мы с вами станем мудрее.
Скачать:
Предварительный просмотр:
Пирогова Татьяна Николаевна г. Таганрог МОУ СОШ № 10.
Тема: «Решение уравнений с модулем и параметром»
10 класс, занятие элективного курса «Свойства функции».
План урока.
- Мотивация.
- Актуализация знаний.
- Решение линейного уравнения с модулем разными способами.
- Решение уравнений содержащих модуль под модулем.
- Исследовательская работа по определению зависимости количества корней уравнения
| | х| - а |= в от значений а и в.
- Рефлексия.
Ход урока.
Мотивация. Как говорили древние философы «Мудрость – это любовь к знаниям, а любовь – это мера всех вещей». «Мера» на латинском языке - «modulus», от него и произошло слово «модуль». И сегодня мы с вами поработаем с уравнениями, содержащими модуль. Надеюсь, у нас все получится, и в конце урока мы с вами станем мудрее.
Актуализация знаний. Итак, вспомним, что мы уже знаем о модуле .
- Определение модуля. Модулем действительного числа – называется само число, если оно неотрицательно и противоположное ему число, если оно отрицательно.
- Геометрический смысл модуля. Модуль действительного числа а равен расстоянию от начала отсчета до точки с координатой а на числовой прямой.
– a 0 a
|– a | = | a | | a | x
- Геометрический смысл модуля разности величин. Модуль разности величин | а – в | - это расстояние между точками с координатами а и в на числовой прямой,
Т.е. длина отрезка [ а в ]
1) Если a b 2) Если a > b
a b b a
S = b – a S = a – b
3) Если a = b , то S = a – b = b – a = 0
- Основные свойства модуля
- Модуль числа есть число неотрицательное, т.е. | x | ≥ 0 для любого x
- Модули противоположных чисел равны, т.е. | x | = |– x | для любого x
- Квадрат модуля равен квадрату подмодульного выражения, т.е. | x | 2 = x 2 для любого x
4. Модуль произведения двух чисел равен произведению модулей сомножителей, т.е.| a b | = | a | · | b |
5. Если знаменатель дроби отличен от нуля, то модуль дроби равен частному от деления модуля числителя на модуль знаменателя, т.е. при b ≠ 0
6. Для равенства любых чисел a и b справедливы неравенства :
| | a | – | b | | ≤ | a + b | ≤ | a | + | b |
| | a | – | b | | ≤ | a – b | ≤ | a | + | b |
- График модуля у = | х | - прямой угол с вершиной в начале координат, стороны которого являются биссектрисами 1 и 2 квадрантов.
- Как построить графики функций? у = | х –4|, у = | х +3|, у = | х –3|, у = | х | + 1 ,
- у = | х | – 3, у = | х | – 5, у = | х – 3 | + 3, у = | х – 3 | – 2, у = | х + 2 | – 5. у = || х| – а |
Пример. Решить уравнение .
Способ 1. Метод раскрытия модулей по промежуткам.
Способ 2. Непосредственное раскрытие модуля.
Если модуль числа равен 3, то это число 3 или -3.
Способ 3 . Использование геометрического смысла модуля.
Необходимо найти на числовой оси такие значения х, которые удалены от 2 на расстояние, равное 3.
Способ 4. Возведение обеих частей уравнения в квадрат.
Здесь используется свойство модуля
И то, что обе части уравнения неотрицательные.
Способ 5. Графическое решение уравнения .
Обозначим. Построим графики функций и :
Абсциссы точек пересечения графиков дадут корни
2 -1 0 1 2 3 |
2 -1 0 1 2 3 4 5 |
2 -1 0 1 2 3 |
2 -1 0 1 2 3 4 5 |
Самостоятельная работа
решите уравнения:
| х – 1| = 3 | х – 5| = 3 | х –3| = 3 | х + 3| = 3 | х + 5| = 3 | (-2; 4) (2; 8) (0; 6) (-6; 0) (-8;-2) |
А теперь добавьте в условия еще один модуль и решите уравнения:
| | х| – 1| = 3 | | х| –5| = 3 | | х | – 3| = 3 | | х | + 3| = 3 | | х | + 5| = 3 | (нет корней) |
Итак, сколько корней может иметь уравнение вида | | х | – а |= в? От чего это зависит?
Исследовательская работа по теме
«Определение зависимости количества корней уравнения | | х | – а |= в от а и в »
Проведем работу по группам, с использованием аналитического, графического и геометрического способов решения.
Определим, при каких условиях данное уравнение имеет 1 корень, 2 корня, 3 корня, 4 корня и не имеет корней.
1 группа (по определению)
2 группа (используя геометрический смысл модуля)
3 группа (используя графики функций)
А > 0 | |||
1 группа | 2 группа | 3 группа |
|
Нет корней | в в ≥ 0 в + а | в в ≥ 0 а + в | в в ≥ 0 в а |
ровно один корень | в > 0 и в + а = 0 | в > 0 и в + а = 0 | в > 0 и в = – а |
ровно два корня | в > 0 и в + а > 0 – в + а | в > 0 и в + а > 0 – в + а | в > 0 и в > | а | |
ровно три корня | в > 0 и – в + а = 0 | в > 0 и – в + а = 0 | в > 0 и в = а |
ровно четыре корня | в > 0 и – в + а >0 | в > 0 и – в + а >0 | в > 0 и в а |
Сравните результаты, сделайте общий вывод и составьте общую схему.
Конечно, необязательно эту схему запоминать . Главное в проведенном нами исследовании было – увидеть эту зависимость, используя разные методы , и теперь повторить свои рассуждения при решении таких уравнений нам будет уже несложно.
Ведь решение задания с параметром всегда подразумевает некоторое исследование.
Решение уравнений с двумя модулями и параметром.
1. Найти значения р, х| – р – 3| = 7 имеет ровно один корень.
Решение: | | х| – (р + 3)| = 7
р +3= -7, р = -10. Или геометрически
р + 3 – 7 р + 3 р + 3+7 р + 3+7=0, р = -10
7 7 по схеме уравнение такого вида имеет ровно один корень, если в = – а, где в =7, а = р +3
2. Найти значения р, при каждом из которых уравнение | | х| – р – 6| = 11 имеет ровно два корня.
Решение: | | х| – (р + 6)| = 11 геометрически
Р + 6 – 11 р + 6 р + 6+11 р + 6-11 р р + 6+11>0, р > -17
11 11
по схеме уравнение такого вида имеет ровно два корня, если в + а > 0 и – в + а где в =11, а = р +6. -17р 5.
3. Найти значения р, при каждом из которых уравнение | | х| – 4 р | = 5 р –9 имеет ровно четыре корня.
Решение: по схеме уравнение такого вида имеет ровно четыре корня, если
0р –9 р, р > и р
т.е. 1 р 9.
Ответ: 1 р 9.
4 . . Найти значения р, при каждом из которых уравнение | | х| – 2 р | = 5 р +2 не имеет корней. Решение: 5 р +2 р +2 =0 и –2 р >0, или 5 р +2 >0 и 5 р +2 р.
р р = –0,4, или р > – 0,4 и р . Ответ : р
5. При каких значениях параметра р уравнение | | х –4 | – 3| + 2 р = 0 имеет три корня. Найти эти корни.
Преобразуем уравнение к виду:
| | х –4 | – 3|= – 2 р .
По схеме уравнение такого вида имеет три корня,
если –2 р =3>0,
Т.е. р = –1,5.
|| х –4|–3| = 3,
| х –4|=0, х = 4,
|| х –4|=6, х = –2, х =10.

Ответ: при р = –1,5 уравнение имеет три корня: х 1 = –2, х 2 = 4, х 3 =10.
Подведение итогов урока. Рефлексия.
Скажите, какие бы вы выделили главные слова урока? (Модуль, параметр)
Что мы сегодня повторили? (Определение модуля, геометрический смысл модуля числа и разности чисел, свойства модуля, разные способы решения уравнений)
Что мы сегодня делали?
Домашнее задание.
Слайд 2
.
Решение уравнений с параметрами и модулями, применяя свойства функций в неожиданных ситуациях и освоение геометрических приемов решения задач. Нестандарные уравнения Цель урока.
Слайд 3
Абсолютной величиной или модулем числа a называется число a, если a>0, число -a, если a 0 ׀ a ׀={ 0, если a=0 -a, если a 0) равносильно двойному неравенству -a 0. Неравенство ׀ х׀>a, (если a>0) равносильно двум неравенствам - Неравенство׀ х׀>a, (если a
Слайд 4
Решить уравнение с параметрами - значит указать, при каких значениях параметров существуют решения и каковы они. а) определить множество допустимых значений неизвестного и параметров; б) для каждой допустимой системы значений параметров найти соответствующие множества решений уравнения. Повторение важнейшего теоретического материала по темам «Решение уравнений с параметрами»
Слайд 5
1. Решить уравнение׀ х-2 ׀ =5; Ответ 7;-3 ׀ х-2 ׀ =-5; Ответ решения нет ׀ х-2 ׀ =х+5; ; Ответ решения нет; 1,5 ׀ х-2 ׀ = ׀ х+5 ׀ ; Ответ решения нет; -1,5; решения нет; -1,5; Устные упражнения.
Слайд 6
2. Решить уравнениеах=1; Ответ. Если a=0, то нет решения;если a=0, тох=1/ a 1.3. Решить уравнение (а²-1) х = а+ 1. 1) а = 1; тогда уравнение принимает вид Ох = 2 и не имеет решения 2) а = 1; получаем Ох = О, и очевидно х - любое. 1 3) если а =± 1 ,то х = -- а-1 Ответ. Если а=-1 , то х- любое; если а=1, то нет решения 1 если а =± 1 ,то х= -- а-1
Слайд 7
2.Решить уравнение׀ х+3 ׀ + ׀ у -2 ׀= 4; . 2 3. 4. 1
Слайд 8
3 3 2 x y 0 1 Ответ: (-3; 2).
Слайд 9
2. Решить уравнениеaх=1;
Ответ. Если a=0, то нет решения; если a=0, то х=1/ a 1.3. Решить уравнение (а²-1) х = а+ 1. 1) а = 1; тогда уравнение принимает вид Ох = 2 и не имеет решения 2) а = 1; получаем Ох = О, и очевидно х - любое. 1 3) если а =± 1 ,то х = -- а-1 Ответ. Если а=-1 , то х- любое; если а=1, то нет решения 1 если а =± 1 ,то х= -- а-1
Слайд 10
3 Построить график функции у= ׀х׀, у= ׀х-2 ׀, у = ׀ х+5I , у = ׀х-2 ׀+3, у = ׀ х+3 ׀-2
y x У=IxI 1 2 -3 -4 -1 1 -2 2 3 0 -5 4 5 6 -1 -2 Y=Ix+3I-2 Y=Ix-2I Y=Ix+5I Y=Ix-2I +3